La distribucion normal, tambien conocida como la distribucion de Gauss o campana de Gauss, es una de las distribuciones mas importantes y ampliamente utilizadas en estadistica. Se caracteriza por tener una forma de campana simetrica y se utiliza para modelar una amplia variedad de fenomenos naturales y sociales.
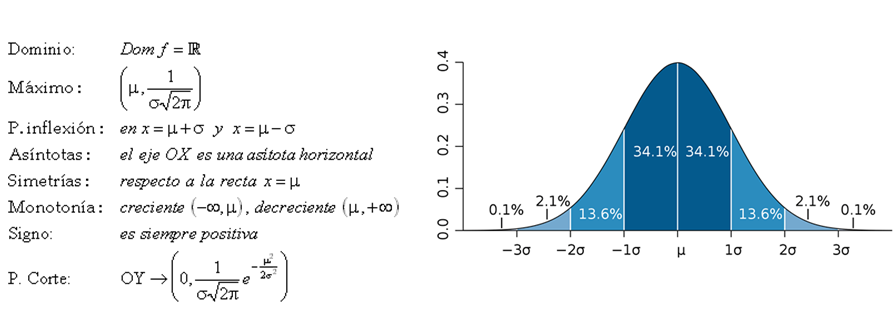
La distribucion normal se define por dos parametros: la media (µ) y la desviacion estandar (s). La media determina la posicion central de la distribucion, mientras que la desviacion estandar indica la dispersion de los datos alrededor de la media. En una distribucion normal estandar, la media es igual a cero y la desviacion estandar es igual a uno.

Una de las propiedades mas importantes de la distribucion normal es la conocida como la regla empirica o regla del 68-95-99.7. Esta regla establece que aproximadamente el 68% de los datos se encuentra dentro de una desviacion estandar de la media, alrededor del 95% se encuentra dentro de dos desviaciones estandar y aproximadamente el 99.7% se encuentra dentro de tres desviaciones estandar.
La distribucion normal es ampliamente utilizada en el analisis de datos y la inferencia estadistica. Muchos fenomenos en la naturaleza y en la sociedad tienden a seguir una distribucion normal, como la altura de las personas, el peso, el rendimiento academico, entre otros. Esta distribucion es especialmente util para describir y analizar la variabilidad y distribucion de datos continuos.
Ademas, la distribucion normal es fundamental en muchos metodos estadisticos, como la estimacion de parametros y la realizacion de pruebas de hipotesis. Se utiliza en diversas disciplinas, como la psicologia, la economia, la fisica, la biologia y muchas otras. La distribucion normal tambien permite realizar transformaciones de datos para que se ajusten a una distribucion mas adecuada.
Esto es util cuando se requiere cumplir con ciertos supuestos estadisticos o cuando se desea comparar diferentes conjuntos de datos. En resumen, la distribucion normal es una distribucion fundamental en estadistica que se utiliza para modelar una amplia gama de fenomenos naturales y sociales. Su forma de campana simetrica y las propiedades asociadas a ella permiten describir y analizar datos continuos de manera efectiva. Esta distribucion es esencial en el analisis de datos y desempena un papel crucial en el campo de la inferencia estadistica
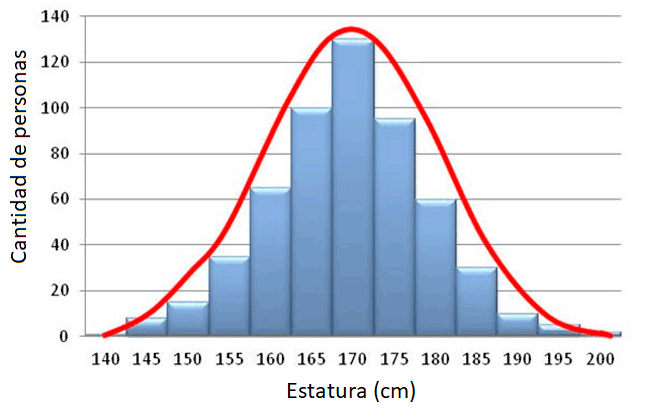
La distribucion normal, tambien conocida como la distribucion de Gauss o campana de Gauss es una de las distribuciones mas importantes y ampliamente utilizadas en estadisticas. Se caracteriza por tener una forma de campana simetrica y se utiliza para modelar una amplia variedad de fenomenos naturales y sociales.
La distribucion normal se define por dos parametros: la media (µ) y la desviacion estandar (s). La media determina la posicion central de la distribucion, mientras que la desviacion estandar indica la dispersion de los datos alrededor de la media. En una distribucion normal estandar, la media es igual a cero y la desviacion estandar es igual a uno.
Una de las propiedades mas importantes de la distribucion normal es la conocida como la regla empirica o regla del 68-95-99.7. Esta regla establece que aproximadamente el 68% de los datos se encuentra dentro de una desviacion estandar de la media, alrededor del 95% se encuentra dentro de dos desviaciones estandar y aproximadamente el 99.7% se encuentra dentro de tres desviaciones estandar.
La distribucion normal es ampliamente utilizada en el analisis de datos y la inferencia estadistica. Muchos fenomenos en la naturaleza y en la sociedad tienden a seguir una distribucion normal, como la altura de las personas, el peso, el rendimiento academico, entre otros. Esta distribucion es especialmente util para describir y analizar la variabilidad y distribucion de datos continuos. Ademas, la distribucion normal es fundamental en muchos metodos estadisticos, como la estimacion de parametros y la realizacion de pruebas de hipotesis. Se utiliza en diversas disciplinas, como la psicologia, la economia, la fisica, la biologia y muchas otras. La distribucion normal tambien permite realizar transformaciones de datos para que se ajusten a una distribucion mas adecuada.
Esto es util cuando se requiere cumplir con ciertos supuestos estadisticos o cuando se desea comparar diferentes conjuntos de datos. En resumen, la distribucion normal es una distribucion fundamental en estadistica que se utiliza para modelar una amplia gama de fenomenos naturales y sociales. Su forma de campana simetrica y las propiedades asociadas a ella permiten describir y analizar datos continuos de manera efectiva. Esta distribucion es esencial en el analisis de datos y desempena un papel crucial en el campo de la inferencia estadistica